Evident, în cazul unui produs vectorial, contează, în plus, ordinea în care sunt luați vectorii,

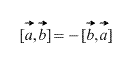
De asemenea, direct din definiție rezultă că pentru orice factor scalar k (număr) este adevărat:

Opera de artă vectorială vectori coliniari este egal cu vectorul zero. Mai mult, produsul încrucișat al doi vectori este zero dacă și numai dacă aceștia sunt coliniari. (În cazul în care unul dintre ele este un vector zero, este necesar să ne amintim că un vector zero este coliniar cu orice vector prin definiție).

Produsul vectorial are proprietate distributivă, adică

Exprimarea produsului vectorial prin coordonatele vectorilor.

Să fie dați doi vectori

(cum se găsesc coordonatele unui vector din coordonatele începutului și sfârșitului său - vezi articolul Produsul punctual al vectorilor, articolul Definiția alternativă a produsului scalar sau calcularea produsului scalar a doi vectori specificati de coordonatele lor.)

De ce aveți nevoie de un produs vectorial?

Există multe modalități de a utiliza produsul încrucișat, de exemplu, așa cum este scris mai sus, calculând produsul încrucișat a doi vectori, puteți afla dacă aceștia sunt coliniari.

Sau poate fi folosit ca o modalitate de a calcula aria unui paralelogram construit din acești vectori. Pe baza definiției, lungimea vectorului rezultat este aria paralelogramului dat.

Există, de asemenea, un număr mare de aplicații în electricitate și magnetism.

Calculator de produse vectoriale online.

Pentru a găsi produsul scalar a doi vectori folosind acest calculator, trebuie să introduceți în prima linie în ordine coordonatele primului vector, în secunda - secunda. Coordonatele vectorilor pot fi calculate din coordonatele începutului și sfârșitului lor (vezi articolul Produsul scalar al vectorilor, element O definiție alternativă a produsului scalar sau calcularea produsului scalar al doi vectori dat de coordonatele lor.)

Opera de artă vectorială este un pseudovector perpendicular pe un plan construit din doi factori, care este rezultatul operației binare „înmulțire vectorială” peste vectori din spațiul euclidian tridimensional. Produsul vectorial nu are proprietățile comutativității și asociativității (este anticomutativ) și, spre deosebire de produsul scalar al vectorilor, este un vector. Utilizat pe scară largă în multe aplicații de inginerie și fizică. De exemplu, momentul unghiular și forța Lorentz sunt scrise matematic ca produs vectorial. Produsul încrucișat este util pentru „măsurarea” perpendicularității vectorilor - modulul produsului încrucișat a doi vectori este egal cu produsul modulelor lor dacă aceștia sunt perpendiculari și scade la zero dacă vectorii sunt paraleli sau antiparaleli.

Produsul vectorial poate fi definit în diferite moduri și, teoretic, într-un spațiu de orice dimensiune n, se poate calcula produsul n-1 vectori, obținând astfel un singur vector perpendicular pe toți. Dar dacă produsul este limitat la produse binare non-triviale cu rezultate vectoriale, atunci produsul vectorial tradițional este definit doar în spații tridimensionale și șapte-dimensionale. Rezultatul unui produs vectorial, ca un produs scalar, depinde de metrica spațiului euclidian.

Spre deosebire de formula pentru calcularea vectorilor de produs scalar din coordonatele unui sistem de coordonate dreptunghiular tridimensional, formula produsului încrucișat depinde de orientarea sistemului de coordonate dreptunghiulare sau, cu alte cuvinte, de „chiralitatea” acestuia.

Definiţie:
Produsul vectorial al vectorului a și al vectorului b în spațiul R3 este un vector c care îndeplinește următoarele cerințe:
lungimea vectorului c este egală cu produsul dintre lungimile vectorilor a și b și sinusul unghiului φ dintre ei:
|c|=|a||b|sin φ;
vectorul c este ortogonal cu fiecare dintre vectorii a și b;
vectorul c este direcționat astfel încât triplul vectorilor abc să fie dreptaci;
în cazul spaţiului R7 se cere asociativitatea triplului vectorilor a, b, c.
Desemnare:
c===a × b

Orez. 1. Aria unui paralelogram este egală cu modulul produsului vectorial

Proprietățile geometrice ale produsului încrucișat:
O condiție necesară și suficientă pentru coliniaritatea a doi vectori nenuli este ca produsul lor vectorial să fie egal cu zero.

Modul încrucișat de produse este egal cu suprafata S paralelogram construit pe vectori reduși la o origine comună oŞi b(vezi Fig. 1).

Dacă e- vector unitar ortogonal cu vectorii oŞi bşi ales astfel încât trei a,b,e- corect, și S este aria paralelogramului construit pe ele (redusă la o origine comună), atunci formula pentru produsul vectorial este valabilă:
=S e

Fig.2. Volumul unui paralelipiped folosind vectorul și produsul scalar al vectorilor; liniile punctate arată proiecțiile vectorului c pe a × b și ale vectorului a pe b × c, primul pas este găsirea produselor scalare

Dacă c- un vector, π - orice plan care conține acest vector, e- vector unitar situat în plan π și ortogonală la c,g- vector unitar ortogonal cu planul π şi direcţionată astfel încât triplul vectorilor ecg este corect, atunci pentru orice culcat în avion π vector o formula este corecta:
=Pr e a |c|g
unde Pr e a este proiecția vectorului e pe a
|c|-modul vectorului c

Când utilizați produse vectoriale și scalare, puteți calcula volumul unui paralelipiped construit pe vectori reduși la o origine comună a, bŞi c. Un astfel de produs de trei vectori se numește mixt.
V=|a (b×c)|
Figura arată că acest volum poate fi găsit în două moduri: rezultatul geometric este păstrat chiar și atunci când produsele „scalare” și „vectorale” sunt schimbate:
V=a×b c=a b×c

Mărimea produsului încrucișat depinde de sinusul unghiului dintre vectorii originali, astfel încât produsul încrucișat poate fi perceput ca gradul de „perpendicularitate” al vectorilor, la fel cum produsul scalar poate fi văzut ca gradul de „paralelism”. ”. Produsul vectorial al doi vectori unitari este egal cu 1 (vector unitar) daca vectorii originali sunt perpendiculari si egal cu 0 (vector zero) daca vectorii sunt paraleli sau antiparaleli.

Exprimarea produsului încrucișat în coordonate carteziene
Dacă doi vectori oŞi b definite prin coordonatele lor carteziene dreptunghiulare sau, mai precis, reprezentate pe o bază ortonormală
a=(a x ,a y ,a z)
b=(b x ,b y ,b z)
iar sistemul de coordonate este dreptaci, atunci produsul lor vectorial are forma
=(a y b z -a z b y ,a z b x -a x b z ,a x b y -a y b x)
Pentru a reține această formulă:
i =∑ε ijk a j b k
Unde ε ijk- simbolul lui Levi-Civita.

PRODUS MIXAT DIN TREI VECTORI ȘI PROPRIETĂȚILE EI

Munca mixta trei vectori se numește număr egal cu . Desemnat . Aici primii doi vectori sunt înmulțiți vectorial și apoi vectorul rezultat este înmulțit scalar cu al treilea vector. Evident, un astfel de produs este un anumit număr.

Să luăm în considerare proprietățile unui produs mixt.

Sensul geometric munca mixta. Produsul mixt a 3 vectori, până la un semn, este egal cu volumul paralelipipedului construit pe acești vectori, ca pe muchii, i.e. .
Astfel, și .

Dovada. Să lăsăm deoparte vectorii din originea comună și să construim un paralelipiped pe ei. Să notăm și să notăm că . Prin definiția produsului scalar

Presupunând că și notând prin h aflați înălțimea paralelipipedului.

Astfel, când

Dacă, atunci așa. Prin urmare, .

Combinând ambele cazuri, obținem sau .

Din demonstrarea acestei proprietăți, în special, rezultă că dacă triplul vectorilor este dreptaci, atunci produsul mixt este , iar dacă este stângaci, atunci .
Pentru orice vector , , egalitatea este adevărată
Dovada acestei proprietăți rezultă din Proprietatea 1. Într-adevăr, este ușor să arătăm că și . Mai mult, semnele „+” și „–” sunt luate simultan, deoarece unghiurile dintre vectorii și și și sunt atât acute, cât și obtuze.
Când oricare doi factori sunt rearanjați, produsul mixt își schimbă semnul.
Într-adevăr, dacă luăm în considerare un produs mixt, atunci, de exemplu, sau
Un produs mixt dacă și numai dacă unul dintre factori este egal cu zero sau vectorii sunt coplanari.
Dovada.

Astfel, o condiție necesară și suficientă pentru coplanaritatea a 3 vectori este ca produsul lor mixt să fie egal cu zero. În plus, rezultă că trei vectori formează o bază în spațiu dacă .

Dacă vectorii sunt dați sub formă de coordonate, atunci se poate demonstra că produsul lor mixt se găsește prin formula:

.

Astfel, produsul mixt este egal cu determinantul de ordinul trei, care are coordonatele primului vector pe prima linie, coordonatele celui de-al doilea vector pe a doua linie și coordonatele celui de-al treilea vector pe a treia linie.

Exemple.

GEOMETRIA ANALITĂ ÎN SPAȚIU

Ecuaţie F(x, y, z)= 0 definește în spațiu Oxyz oarecare suprafață, adică locul punctelor ale căror coordonate x, y, z satisface această ecuație. Această ecuație se numește ecuația suprafeței și x, y, z– coordonatele curente.

Cu toate acestea, adesea suprafața nu este specificată printr-o ecuație, ci ca un set de puncte din spațiu care au una sau alta proprietate. În acest caz, este necesar să găsiți ecuația suprafeței pe baza proprietăților sale geometrice.

AVION.

VECTOR PLAN NORMAL.

ECUAȚIA UNUI AVION PENTRU UN PUNCT DATE

Să considerăm un plan arbitrar σ în spațiu. Poziția sa este determinată prin specificarea unui vector perpendicular pe acest plan și a unui punct fix M0(x 0, y 0, z 0), situată în planul σ.

Se numește vectorul perpendicular pe planul σ normal vector al acestui plan. Fie vectorul să aibă coordonate.

Să derivăm ecuația planului σ care trece prin acest punct M0și având un vector normal. Pentru a face acest lucru, luați un punct arbitrar pe planul σ M(x, y, z)și luați în considerare vectorul .

Pentru orice punct MО σ este un vector Prin urmare, produsul lor scalar este egal cu zero. Această egalitate este condiția ca punctul MО σ. Este valabil pentru toate punctele acestui plan și este încălcat de îndată ce punctul M va fi în afara planului σ.

Dacă notăm punctele cu vectorul rază M, – raza vectorului punctului M0, atunci ecuația poate fi scrisă sub forma

Această ecuație se numește vector ecuația plană. Să-l scriem sub formă de coordonate. De atunci

Deci, am obținut ecuația planului care trece prin acest punct. Astfel, pentru a crea o ecuație a unui plan, trebuie să cunoașteți coordonatele vectorului normal și coordonatele unui punct situat pe plan.

Rețineți că ecuația planului este o ecuație de gradul I în raport cu coordonatele curente x, yŞi z.

Exemple.

ECUAȚIA GENERALĂ A AVIONULUI

Se poate arăta că orice ecuație de gradul I în raport cu coordonatele carteziene x, y, z reprezintă ecuația unui plan. Această ecuație se scrie astfel:

Ax+By+Cz+D=0

si se numeste ecuație generală planul și coordonatele A, B, C aici sunt coordonatele vectorului normal al planului.

Să luăm în considerare cazuri speciale ale ecuației generale. Să aflăm cum este situat planul în raport cu sistemul de coordonate dacă unul sau mai mulți coeficienți ai ecuației devin zero.

A este lungimea segmentului tăiat de planul de pe axă Bou. În mod similar, se poate demonstra că bŞi c– lungimi ale segmentelor tăiate de planul luat în considerare pe axe OiŞi Oz.

Este convenabil să folosiți ecuația unui plan în segmente pentru a construi planuri.

Definiţie. Produsul vectorial al vectorului a și vectorului b este un vector notat cu simbolul [α, b] (sau l x b), astfel încât 1) lungimea vectorului [a, b] este egală cu (p, unde y este unghiul dintre vectorii a și b ( Fig. 31 2) vectorul [a, b) este perpendicular pe vectorii a și b, i.e. perpendicular pe planul acestor vectori; 3) vectorul [a, b] este direcționat în așa fel încât de la sfârșitul acestui vector cea mai scurtă rotație de la a la b se vede că are loc în sens invers acelor de ceasornic (Fig. 32). Orez. 32 Fig.31 Cu alte cuvinte, vectorii a, b și [a, b) formează un triplet din dreapta de vectori, i.e. dispuse ca degetul mare, arătător și mijlociu mâna dreaptă. Dacă vectorii a și b sunt coliniari, vom presupune că [a, b] = 0. Prin definiție, lungimea produsului vectorial este egală numeric cu aria Sa a unui paralelogram (Fig. 33), construit pe baza multiplicată. vectorii a și b ca laturi: 6.1 . Proprietăţile unui produs vectorial 1. Un produs vectorial este egal cu vectorul zero dacă şi numai dacă cel puţin unul dintre vectorii înmulțiți este zero sau când acești vectori sunt coliniari (dacă vectorii a și b sunt coliniari, atunci unghiul dintre ei este fie 0, fie 7r). / Dacă punctele O, A, B, C nu se află în același plan (vectorii a, b și c sunt necoplanari), vom construi un paralelipiped pe muchiile OA, OB și OS (Fig. 38 a). Prin definiția unui produs vectorial, avem (a,b) = So c, unde So este aria paralelogramului OADB și c este vectorul unitar perpendicular pe vectorii a și b și astfel încât triplul a , b, c este dreptaci, i.e. vectorii a, b și c sunt localizați, respectiv, ca degetul mare, arătător și mijlociu ale mâinii drepte (Fig. 38 b). Înmulțind scalar ambele părți ale ultimei egalități din dreapta cu vectorul c, obținem că produsul vectorial al vectorilor dat de coordonate. Munca mixta. Numărul pc c este egal cu înălțimea h a paralelipipedului construit, luată cu semnul „+” dacă unghiul dintre vectorii c și c este ascuțit (triplu a, b, c - dreapta), și cu „-” semn dacă unghiul este obtuz (triplu a, b, c - stânga), astfel încât. Astfel, produsul mixt al vectorilor a, b și c este egal cu volumul V al paralelipipedului construit pe acești vectori ca pe muchii, dacă triplul a, b, c este drept și -V, dacă triplul a , b, c - stânga. Pe baza semnificației geometrice a produsului mixt, putem concluziona că înmulțind aceiași vectori a, b și c în orice altă ordine, vom obține întotdeauna fie +7, fie -K. Marca producătorului Fig. 38 de referință va depinde doar de ce fel de triplu formează vectorii înmulțiți - dreapta sau stânga. Dacă vectorii a, b, c formează un triplu dreptaci, atunci triplele b, c, a și c, a, b vor fi și ele dreptaci. În același timp, toate cele trei triple b, a, c; a, c, b și c, b, a - stânga. Astfel, (a,b, c) = (b,c, a) = (c,a,b) = -(b,a,c) = -(a,c,b) = -(c,b , O). Subliniem din nou că produsul mixt al vectorilor este egal cu zero numai dacă vectorii înmulțiți a, b, c sunt coplanari: (a, b, c sunt coplanari) 7.2. Produs mixt în coordonate Fie vectorii a, b, c dați de coordonatele lor în baza i, j, k: a = (x\,y\,z]), b= (x2,y2>z2), c = (x3, uz, 23). Să găsim o expresie pentru produsul lor mixt (a, b, c). Avem un produs mixt de vectori specificați prin coordonatele lor în baza i, J, k, egal cu determinantul de ordinul trei, ale căror linii sunt compuse, respectiv, din coordonatele primului, al doilea și al treilea dintre vectorii înmulțiți. Condiția necesară și suficientă pentru coplanaritatea vectorilor a y\, Z|), b = (хъ У2.22), с = (жз, з, 23) se va scrie sub următoarea formă У| z, ag2 y2 -2 =0. Uz Exemplu. Verificați dacă vectorii „ = (7,4,6), b = (2, 1,1), c = (19, II, 17) sunt coplanari. 7.3. Produsul dublu încrucișat Produsul dublu încrucișat [a, [b, c]] este un vector perpendicular pe vectorii a și [b, c]. Prin urmare, se află în planul vectorilor b și c și poate fi extins în acești vectori. Se poate arăta că formula [a, [!>, c]] = b(a, e) - c(a, b) este valabilă. Exerciţii 1. Trei vectori AB = c, Ж? = o și CA = b servesc drept laturi ale triunghiului. Exprimați în termeni de a, b și c vectorii care coincid cu medianele AM, DN, CP ale triunghiului. 2. Ce condiție trebuie să fie legați vectorii p și q astfel încât vectorul p + q să împartă unghiul dintre ei la jumătate? Se presupune că toți cei trei vectori sunt legați de o origine comună. 3. Calculați lungimea diagonalelor unui paralelogram construit pe vectorii a = 5p + 2q și b = p - 3q, dacă se știe că |p| = 2v/2, |q| = 3H-(p7ci) = f. 4. Notând cu a și b laturile rombului care se extind de la vârful comun, demonstrați că diagonalele rombului sunt reciproc perpendiculare. 5. Calculați produsul scalar al vectorilor a = 4i + 7j + 3k și b = 31 - 5j + k. 6. Aflați vectorul unitar a0 paralel cu vectorul a = (6, 7, -6). 7. Aflați proiecția vectorului a = l+ j- kHa vector b = 21 - j - 3k. 8. Aflați cosinusul unghiului dintre vectorii IS “w, dacă A(-4,0,4), B(-1,6,7), C(1,10,9). 9. Aflați vectorul unitar p°, care este simultan perpendicular pe vectorul a = (3, 6, 8) și pe axa Ox. 10. Calculați sinusul unghiului dintre diagonalele paralelogramului construit pe vectorii a = 2i+J-k, b=i-3j + k ca pe laturi.

Semnificațiile cărților de tarot